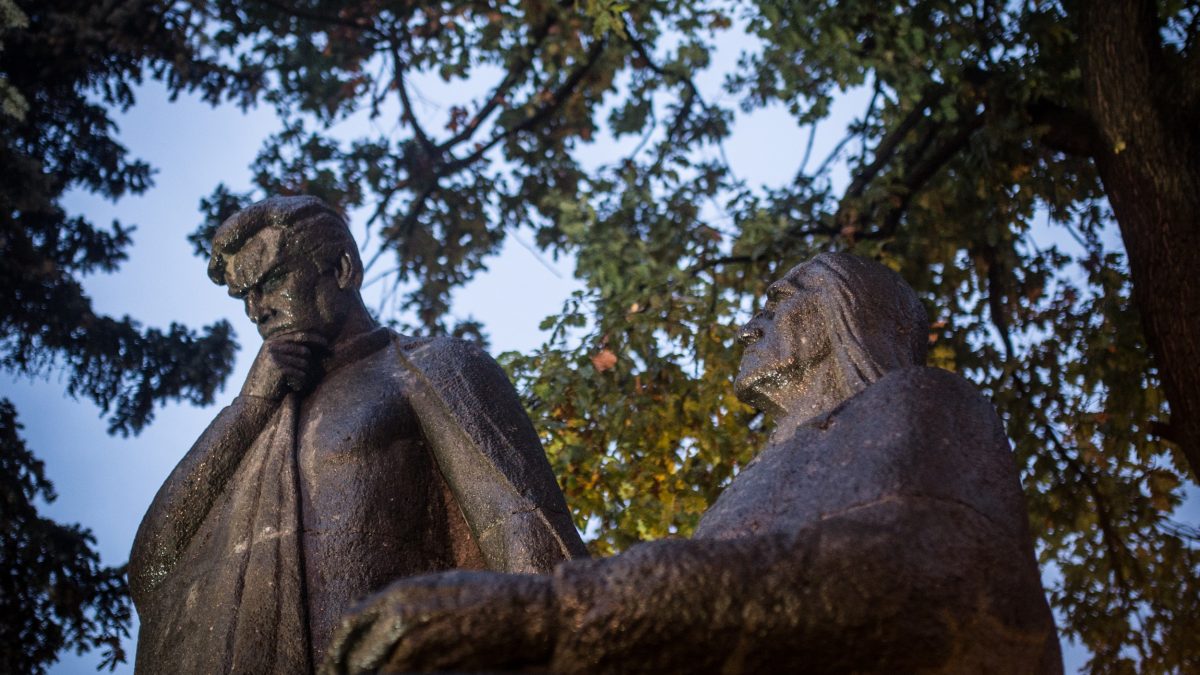A mindenség elméletét kezdte írni, mégis elfeledetten halt meg az első magyar zseni
Ha nagy, korszakalkotó magyar természettudósokról beszélünk, Teller Edére, Neumann Jánosra vagy 20. századi Nobel-díjasainkra gondolunk. Pedig jóval előttük élt egy erdélyi matematikus, aki az emberi gondolkodás történetének egyik legragyogóbb eredményét érte el. Bolyairól sok mindent neveztek el, de a legtöbbször azt sem tudjuk, hogy Farkasról vagy Jánosról. Leérettségizünk anélkül, hogy egy szót hallanánk gondolataiból. Most új regény állítja középpontba Bolyai János hányattatott életét. Láng Zsolt könyvéből egy olyan tudós képe bontakozik ki, aki a teljes elutasítottság dacára sem adta fel hitét, hogy a természet titkai megfejthetők, és a tudás a boldogság szolgálatába állítható.
„Drága Apám!
(…) Ami pedig a kibaszott kardtartást illeti, szeretném megjegyezni, hogy az összes nekem adott tanácsa hülyeség volt, ez valamennyinél bebizonyosodott. Azt mondta, ne foglalkozzam a párhuzamossággal, aztán mégis a könyvében prezentálta a munkámat, mintha a maga műve volna. Azt mondta, hogy a komplex számoknak nincs szerepük a pályaívek meghatározásánál, mégis, amikor én rájöttem, hogy igen, maga is igenelni kezdett. Amikor kiszámoltam a sinus és a cosinus faktoriálisát, azt mondta, tévedtem, aztán mégis átvette a szögfelezők tételéhez. Amit a lipcseieknek írtam, azt mondta, nem ér semmit, de bátorkodom, hajlok rá akármibe fogadni, felrakom Domáldot ellenében, hogy húsz év múlva az én bizonyításom általános lesz, a magáét elsüllyesztik a feledésbe, és ezzel jól fog járni, mert legalább nem tudják kiröhögni.”
Láng Zsolt Bolyai című regényének egyik legizgalmasabb szála a Bolyai Jánost édesapjához, Farkashoz fűző kapcsolat. Két nagyon eltérő személyiségű lángelme képe rajzolódik ki. „Farkas az a zseni, aki társasági ember, leveszi a lábáról a hallgatóságot” – mondja az író. „A fia pedig az a zseni, aki prímszámokban számolja a lépéseit, és szinte tudomást sem vesz a világról azon a problémán kívül, ami éppen foglalkoztatja.” Apa és fia állandóan vitatkozik. Farkas hol János kicsapongónak vélt életmódját, hol a kis családi birtokon, Domáldon folytatott hanyag gazdálkodását rója fel neki. Mégis bátran állíthatjuk, hogy édesapja a legfontosabb ember volt Bolyai János életében. Ő volt az egyetlen ugyanis, aki megértette.
Bolyai János hiába tette a matematika történetének egyik legnagyobb felfedezését, életében ezért sem anyagi, sem erkölcsi elismerést nem kapott. „Talentuma használatlanul ásatott el” – jegyezték róla fel az anyakönyvbe temetése után,
ahol a kötelező katonai kíséreten kívül mindössze három civil vett részt. Nagy műve, a nemeuklideszi geometria a 19. század Erdélyén és Magyarországán terméketlen táptalajra hullott. Felfedezését kortársai vagy nem értették, vagy el sem olvasták. Korszakalkotó értekezését a Magyar Tudós Társaságnak is elküldte, de ott csak a polcon porosodott, s mivel latinul, nem magyarul publikált, fel sem vetődött, hogy az Akadémia elődje akár csak levelező tagjává válassza. Aki értette felfedezését, Gauss, „a matematika fejedelme”, elhallgatta eredményeit. Ha nincs Bolyai Farkas, János senkivel sem tudott volna matematikáról beszélni. Apja utolsó éveiben megbékéltek, s János 1911-es újratemetése óta egymás mellett nyugszanak a marosvásárhelyi református temetőben.
Alexandria, Göttingen, Erdély
Történünk az ókori Hellászban indul. A görög tudósok az egyiptomi földmérők (geométerek) tapasztalatainak rendszerezésével megalkotják a geometriát. Alexandriai Eukleidész Kr. e. 300 körül Elemek című nagy munkájában foglalja össze a tudományt. A könyv kétezer éve alapja geometriai ismereteinknek. Ez az a geometria, amelyet az iskolában megtanulunk: amelyben a háromszög szögeinek összege 180 fok, és ahol a párhuzamosok sohasem találkoznak. Igaz, utóbbi állítás nem olyan magától értetődő, mint Eukleidész többi állítása. Nem tudunk végtelen vonalakat húzni, s így tapasztalati úton ellenőrizni – az állítás bizonyításra szorul. A bizonyítást kétezer éven át sokan megpróbálják, de senkinek sem sikerül.
Az egyikük Bolyai Farkas. Elszegényedett erdélyi kisnemesi család sarja, de egy báró a fia mellé veszi tanulótársnak. A vallásszabadsághoz szokott erdélyiek akkoriban a híres német egyetemre, a gondolat szabadságát a legkevésbé korlátozó göttingenibe vágynak. Bolyaiék is itt kötnek ki 1796 és 1799 között. Nagyjából ekkor jár Göttingenbe Carl Friedrich Gauss is, és Farkas barátságot köt vele. Hazatérve a vásárhelyi református kollégium tanára lesz, és életét Eukleidész 5. posztulátuma – a párhuzamossági axióma – bizonyítására teszi fel. Hogy mekkora sikerrel, jelzi a fiához írt 1820-as intelme:
„Az Istenért kérlek! Haggy békét a paralleláknak, úgy irtozz tölle, mint akarmitsoda feslett társalkodástól, éppen úgy megfoszthat (mint engem) minden idődtől, egésségedtől, tsendességedtől, s egész életed boldogságától.”
Nem tudhatta, hogy az axiómát nem lehet bizonyítani, s erre fia jön majd rá.
János az intelem idején a bécsi Császári és Királyi Hadmérnöki Akadémia hallgatója. Erdélyben ekkor még nem volt egyetem, Pesten pedig nem volt olyan professzor, aki a 14 évesen már a differenciál- és integrálszámítást is kisujjból kirázó Jánosnak újat mondhatott volna. Göttingeni taníttatásának költségeit apja nem tudta kifizetni, a továbbtanulás egyetlen útja a katonai pálya volt. János tíz éven át szolgál hadmérnökként, nem túl nagy lelkesedéssel. A párhuzamosokkal volt ő is elfoglalva, fittyet hányva az atyai tanácsra. „Mihelyt rendbe szedem, el-készítem, s mód leszsz, a parallelákról egy munkát adok ki; (…) ha meg-látja Édes Apám meg-esméri; most többet nem szólhatok, tsak annyit: hogy semmiből egy ujj más világot teremtettem” – írja.
Mi ez a más világ? Képzeljünk el egy papírlapon egy egyenest, amire merőlegeseket rajzolunk. Az euklideszi geometriában, mint tudjuk, ezek a merőlegesek sohasem metszik egymást. Most képzeljük el ugyanezt egy gömbfelületen. Legyen az egyenes mondjuk az Egyenlítő, a rá rajzolt merőlegesek pedig a hosszúsági fokok. Mint tudjuk, ezek igenis találkoznak: az Északi- és a Déli-sarkon. Most pedig képzeljünk el egy nyerget, vagy egy burgonyachipset. Ezek görbült felületén az egyenesre rajzolt merőlegesek nemhogy nem találkoznak, de éppen távolodnak egymástól. Míg a papírlapon a háromszög szögösszege 180 fok, a gömbfelületen több, a hiperbolikus felületen (a nyergen és a chipsen) pedig kevesebb. Ezzel el is képzeltük a három alapvető geometriát, az euklideszit (papírlap), a riemannit (gömb) és a Bolyai–Lobacsevszkij-félét (nyereg).
Bolyai megalkotta azt az elméleti keretet is, amely az euklideszi és a hiperbolikus geometriát is magába foglalja – ez az abszolút geometria.
A magányos zseni
„Bolyai tudományos munkája a XIX. század egyik legnagyobb matematikai eredménye, ő maga minden idők egyik legnagyobb matematikusa volt” – mondja a Válasz Online-nak Szabó Péter Gábor tudománytörténész. Bolyai felfedezésének még nagyobb jelentősége volt. Az ugyan városi legenda, hogy Einsten az I. világháború előtt Marosvásárhelyen járt, és elvitte Bolyai relativitáselméletről írt kéziratát, de az igaz, hogy a nemeuklideszi terek fontos matematikai alapját képezték a 20. századi fizikának, a relativitáselméletnek és a kvantumfizikának. Sőt, Bolyai is megsejthette, hogy magának a fizikai térnek a szerkezete sem feltétlenül euklideszi. Már apja felvetette, hogy a tér természetére a bolygók mozgásából lehetne következtetni. János pedig még tovább ment egy nem newtoni gravitációs törvény megfogalmazásával. Egyik papírfecnire vetett kézirattörekében pedig még azt is felveti, hogy „az nehézkedés törvénye is szoros összveköttetésben, foljtatásban tetszik az űr természetével, valójával, miljségével.”
A nemeuklideszi geometria kibontása Bolyai Farkas Testamen című összefoglaló művének függelékeként (Appendix) jelent meg 1830-ban. Egy példányt Farkas kiküldött barátjának, Gaussnak, de a válasz lesújtó volt. „Most valamit a fiad munkájáról. Ha azzal kezdem, hogy nem szabad dicsérnem: bizonyára meghökkensz egy pillanatra. Mást azonban nem tehetek: ha dicsérném, akkor magamat dicsérném, mivel a mű egész tartalma, az út, melyet fiad követ és az eredmények, amelyekre jutott, majdnem végig megegyeznek részben már 30-35 év óta folytatott elmélkedéseimmel.” Igaz, Gauss nem publikálta ezeket az elmélkedéseit, mivel félt a kortársak elítélő válaszától – a nemeuklideszi geometria ugyanis látszólag szembement a német felvilágosodás vezető alakja, az általa is ájulásig tisztelt Immanuel Kant térfilozófiájával.
Bolyai János ezzel szemben nagyon is méltányosan bánt azzal az orosz tudóssal, aki vele közel egy időben, tőle függetlenül tett azonos felfedezést. „Én örömest megosztom a találói érdemet” – írta 1844-ben, amikor először került a kezébe Nyikolaj Ivanovics Lobacsevszkij dolgozata. Bolyai érdemeinek elismerése csak Gauss halála után, az ő hagyatékának feldolgozása után indult el – magánleveleiben ugyanis nem szégyellte lángésznek nevezni. A századfordulóra nagyjából a helyére került Bolyai. „Az UNESCO az Appendix 1831-es példányát felvette a Világemlékezet Listájára, viszont az is elő szokott fordulni, hogy még maguk a matematikusok is keveset tudnak a Bolyaiakról – mondja Szabó Péter Gábor. – Sajnos tudnék mutatni olyan híres számítógépes matematikai programcsomagot is, amely a hiperbolikus geometriát ma is egyszerűen Lobacsevszkij-geometriának mondja.”

A tudománytörténész szerint azzal is sokat tehetnénk azért, hogy Bolyai az őt megillető helyre kerülne, ha bekerülne a középiskolai tananyagba. „Fontos is lenne, hogy egy érettségizett magyar ember tudjon valamit Bolyai János geometriájáról – mondja. – A számelmélet terén hasonló jellegű kitekintést mindenki kap, hiszen tanul arról, hogy nemcsak a tízes számrendszer létezik. Ugyanígy érdemes lenne betekintést kapniuk a diákoknak arról is, hogy nemcsak az euklideszi geometria létezik. Egymás mellett szerepeltetni az euklideszi, a gömbi és a Bolyai-Lobacsevszkij-féle geometriákat, különféle modelleken szemléltetni ezeket meghatározó élménye lehet az érdeklődő fiataloknak, ami a világlátásukra is hatással lehet.
Az ember ilyenkor rájöhet arra, hogy a másik embernek is igaza lehet a saját gondolati világán belül, még akkor is, ha az ő eredménye esetleg ellentmond annak, amit saját maga hirdet.”
Nemeuklideszi regény
Azért nem ismeretlen Bolyai: iskolák, tudományos díjak, matematikai versenyek viselik a nevet. Még egy kisbolygót is elnevezett róla egy magyar csillagász, jóllehet a lajstromba tévedésből Farkast jegyeztek be. Számos irodalmi mű is született róla, igaz, gyakran torz képet festettek ezek. „Nemigen akad olyan regényíró, aki Bolyai János geometriáját (…) megértené és azt beépíteni tudná regénye vázába – írta Weszely Tibor. „Így nem közelíthetve az alkotáslélektan mélyebb régióit, marad számára a fantáziát élénkítőbb, felszínen érvényesülő (vagy képzelt) tulajdonságok dramatizálása. Ördöghegedűs párbajhős, »vadházasságban« élő mogorva vadóc, apjára kardot rántó fiú kétségtelenül regényesebb alak, mint a párhuzamosokra vonatkozó, több mint kétezer éves problémán töprengő mérnökkari tiszt.”
Mindennek volt valóságalapja. Élettársát, Orbán Rozáliát, akitől két gyermeke is született, nem tudta elvenni, mivel a katonatisztek számára házasság esetére előírt kauciót nem tudták előteremteni. Tényleg virtuóz hegedűjátékos volt, és olykor párbajozott is. Ugyanakkor az életmű fokozatos feldolgozásával születtek jelentősebb művek is, például Németh László A két bolyai című 1960-as drámája. Babits Mihály 1911-es szonettje máig borzongató.

A kortárs magyar irodalom azonban évek óta görgeti maga előtt egy Bolyai-regény megírását. „Most, hogy Esterházy meghalt, ki fogja megírni a Bolyai-regényt?” – kérdezi Krasznahorkai László Láng Zsoltot a most megjelent regényben. Az ugyanis a klasszikus kriminarratológiát követve nemcsak Bolyairól szól, hanem arról a nyomozásról is, amelyet az író folytat Bolyai után. Míg az egyik szálon a matematikus életének egy-egy epizódjában pillantunk bele a gondolataiba, a másikon Láng Zsoltot követjük, ahogy egy svájci kolostorban Bolyai kéziratait tanulmányozza. Esterházy Péter egy marosvásárhelyi látogatásán botlott bele a Teleki Tékában őrzött, mintegy 14 ezer oldalas, matematikai értekezéseket és leveleket, papírfecniket és teleírt koncertlapokat egyaránt tartalmazó Bolyai-hagyatékba. Esterházynak végül nem adatott meg, hogy megírja a Bolyai-regényt, Láng Zsolt azonban vállalkozott a feladatra.
„A leginkább az Üdvtannak vagy Világtannak nevezett terve foglalkoztatott, amit harminc éven át próbált megírni – vallja az író. – Az alapképletet akarta megfogalmazni, ami magába sűrítené mindezt, ami a világra jellemző. A matematika mellett ugyanis nyelvészettel, zeneelmélettel, morálfilozófiával is foglakozott.” Az Üdvtanhoz írt jegyzetekből egy mai szemmel olykor megmosolyogtatóan naiv utópia bontakozik ki, amely azonban nagyon is illik a felvilágosodás idején született racionalista utópiák sorába. A felvázolt ideális társadalomban nincs pénz, a fegyvereket elveszik a katonáktól, az embereket név helyett számokkal nevezik meg, és minden egészséges ember köteles napi két órában művelni a köztulajdonban álló földet. „A rokonszenv és részvét helyébe a józan okosságnak kell lépnie. Nem nógatás, nem törvény, nem parancs, nem erőszak kell, hanem művelés ellenállhatatlan varázserejének a hatalmánál fogva a közüdv magától bekövetkezik” – írja. Hasonló gondolatokat nem más, mint Gauss szájába ad A világ fölmérése című 2013-as regényében Daniel Kehlmann német író.
Noha Láng Zsolt könyve is gazdag a humorban, iróniában, nem leplezett tisztelettel viseltetik Bolyai optimizmusa, a világ fölmérésére irányuló lelkesedése iránt. „Bolyainak a legfontosabb, hogy tényekkel és számokkal leírja a világot. Ma mindez meg van kérdőjelezve, a tények nem fontosak. De az írás közben ellátogattam Svájcban a Nagy Hadronütköztetőbe, és azt láttam, hogy tízezer ember ügyködik a világ megértésén, úgy, ahogy Bolyai is tette – idézi fel a szerző. „Az írás megerősítette bennem, hogy a világ nem zárkózik el attól, hogy az ember megismerje, és nem ellenünk van, hanem valamiképp a pártunkon áll.”
Nyitókép: a Bolyaiak szobra Marosvásárhelyen (Izsák Márton és Csorvássy István alkotása, 1957). Fotó: Vörös Szabolcs